Regulator: A unique method of subdomain enumeration

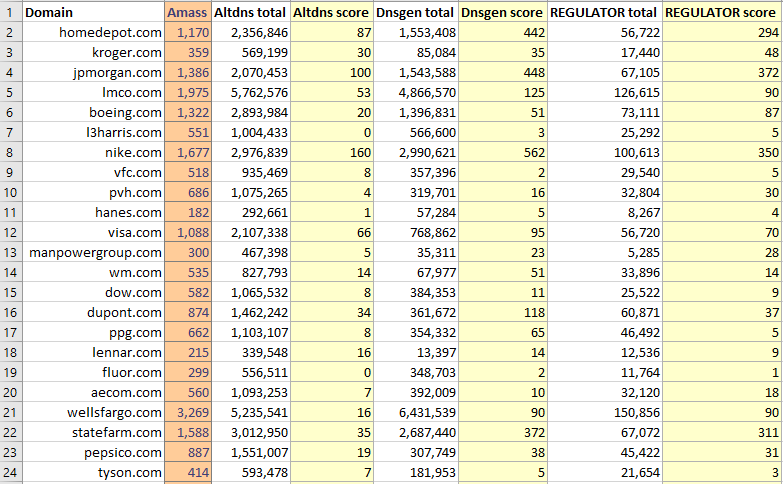
# Introduction

To state the obvious: subdomain enumeration is where we want to find subdomains
for a set of top-level domains scoped to a target. Subdomain enumeration is just
one small part of a larger reconnaissance process that is typically the first
phase of a penetration test or Red Team.

There are a lot of different ways to do subdomain enumeration, but I want to
show you a unique method that I can almost guarantee you've never seen before.

In a [previous blog post](https://cramppet.github.io/dank/index.html), I
introduced `dank` and showed how it's unique encoding mechanism can be used to
encode shellcode for use in implants and loaders.

In this blog post, I'll explore another use case of `dank` whereby we combine
the idea of regular language **ranking** with [regular language
induction](https://en.wikipedia.org/wiki/Induction_of_regular_languages).

Our goal is to be able to *automagically* learn regexes that capture
idiosyncratic features of observed DNS data. Using these learned patterns, we
will attempt to brute force for new subdomains that follow these same patterns.

I'll show that experimentally, this method seems to be highly effective compared
to other industry-known tools such as `altdns`.

I've called this project "regulator" and [you can find it on my GitHub
here](https://github.com/cramppet/regulator)

**Note:** There is a decent amount of hand-waving here and "it just works"
mentality, although I'll try my best to explain *why* it works as we go along,
in reality, I don't have a formal, technical answer.

# TL;DR

1. We collect as much DNS data as we can using existing tools: `amass`,
`subfinder`, etc.

2. We induce regular languages from this observed DNS data

3. We use these languages (regexes) to synthesize new DNS hostnames

4. We evaluate the results against similar tools such as: `altdns` and `dnsgen`

# Collecting initial data

This process relies heavily on the initial input data, so you should spend some
time ensuring you've captured everything that you can from existing
tools/methods.

It's also worth pointing out that this process is not intended for small domains
(ie. less than about 100 subdomains) because other tools like dictionary brute
forcers will usually work far better.

# Inducing languages

The process is complex and is best summarized by reading the code linked above.
For brevity, the critical function is `closure_to_regex`:

```python
def closure_to_regex(domain: str, members: List[str]) -> str:
  """converts edit closure to a regular language"""
  ret, levels, optional = '', {}, {}
  tokens = tokenize(members)
  for member in tokens:
    for i, level in enumerate(member):
      if i not in levels:
        levels[i] = {}
        optional[i] = {}
      for j, token in enumerate(level):
        if not j in levels[i]:
          levels[i][j] = set([])
          optional[i][j] = []
        levels[i][j].add(token)
        optional[i][j].append(token)
  for i, level in enumerate(levels):
    n = '(.' if i != 0 else ''
    for j, position in enumerate(levels[level]):
      k = len(levels[level][position])
      # Special case: first token in DNS name
      if i == 0 and j == 0:
        n += f"({'|'.join(levels[level][position])})"
      # Special case: single element in alternation at start of level
      elif k == 1 and j == 0:
        # TODO: Should we make this optional too?
        n += f"{'|'.join(levels[level][position])}"
      # General case
      else:
        # A position is optional if some token doesn't have that position
        isoptional = len(optional[level][position]) != len(members)
        n += f"({'|'.join(levels[level][position])}){'?' if isoptional else ''}"
    # A level is optional if either not every host has the level, or if there 
    # are distinct level values
    values = list(map(lambda x: ''.join(x), zip(*optional[level].values())))
    isoptional = len(set(values)) != 1 or len(values) != len(members)
    ret += (n + ")?" if isoptional else n + ")") if i != 0 else n
  return compress_number_ranges(f'{ret}.{domain}')
```

If you know anything about language induction, you're probably very confused.
That's because what I've shown above is not a formal method of inducing regular
languages like **L-star** or **RPNI**, instead it's a simple heuristic function.

This has seemed to work well though, because the data we're working with is
simple and is usually highly structured. Here's what the function above does:

- Given that you have:
  - `foo1-dev.example.com`
  - `foo2-prod.example.com`
  - `foo5-qa.example.com`

- The function tokenizes these instances into:
  - `[foo1, dev, example, com]`
  - `[foo2, prod, example, com]`
  - `[foo5, qa, example, com]`

- Then it recombines them into patterns or "rules" where shared "levels" are
merged: `(foo1|foo2|foo5)-(dev|qa|prod).example.com`

- Finally, it analyzes numerical values and converts them into ranges (if
possible): `(foo[1-5])-(dev|qa|prod).example.com`

Looking at the final rule obtained, we can see that there are new names not
previously observed that are a part of the regular language we inferred:

- `foo1-qa.example.com`
- `foo2-dev.example.com`
- `foo3-prod.example.com`
- ...

It is precisely these new language members that constitute our brute force
attempts. There is a lot more that can be said about what we do here, but I
don't want to dwell on this too much, as it is likely just too much information
for this post.

# Synthesizing new names

The process of generating new names from our regex rules is simply the process
of enumerating all language members and deduplicating against what we already
observed.

The first part can be done using the `DankGenerator` class from the `dank`
package, the latter part is done using set difference (ie. `A - B`).

```python
>>> from dank.DankGenerator import DankGenerator
>>> for i in DankGenerator('(foo[1-5])-(dev|qa|prod).example.com'):
...     print(i)
...
b'foo5-qa.example.com'
b'foo4-qa.example.com'
b'foo3-qa.example.com'
b'foo2-qa.example.com'
b'foo1-qa.example.com'
b'foo5-dev.example.com'
b'foo4-dev.example.com'
b'foo3-dev.example.com'
b'foo2-dev.example.com'
b'foo1-dev.example.com'
b'foo5-prod.example.com'
b'foo4-prod.example.com'
b'foo3-prod.example.com'
b'foo2-prod.example.com'
b'foo1-prod.example.com'
```

One of things that became apparent when developing regulator is that we need
some kind of filtering criteria for our rules. Basically, some rules will
produce a literal astronomical amount of language members and we don't want the
number of guesses we perform to be much more than 1,000,000. Thus, we need a way
to filter out certain rules.

What I settled on was a simple ratio test. The logic being that the number of
observed language members should not increase beyond a certain integer multiple,
the default value being 25. This means that if we observed 10 hosts to produce a
rule, then the rule could contain up to 250 language members before being
filtered -- this has seemed to work extremely well at capturing "good guesses"
without blowing out the total number of guesses.

# A real-world example: `adobe.com`

## Data collection

I collected the initial data using `amass` with the `-brute` flag. This took a
while, but after it was finished we had `1960` hosts.

We can run the regulator script to generate rules for this input:

```
python3.8 main.py adobe.com adobe adobe.rules
```

## Inducing languages

You can look at the log file stored in `logs/` to see the progress of what is
happening:

```
2022-10-16 12:16:30,702 - root - INFO - REGULATOR starting: MAX_RATIO=25.0, THRESHOLD=500
2022-10-16 12:16:30,706 - root - INFO - Loaded 1960 observations
2022-10-16 12:16:30,706 - root - INFO - Building table of all pairwise distances...
2022-10-16 12:16:34,594 - root - INFO - Table building complete
2022-10-16 12:16:34,594 - root - INFO - k=2
2022-10-16 12:16:36,733 - root - INFO - k=3
2022-10-16 12:16:38,761 - root - INFO - k=4
2022-10-16 12:16:41,900 - root - INFO - k=5
```

The memoization table being built is a table of pairwise [Levenshtein
distances](https://en.wikipedia.org/wiki/Levenshtein_distance) between all 1960
observations.

This common string metric is used to define the concept of a "Levenshtein
closure" -- this is what is meant by a "closure" in `closure_to_regex`: a set of
hostnames bounded by some fixed Levenshtein distance.

Once the memoization has completed, we can see more output from the tool:

We use a prefix tree [also known as a Trie](https://en.wikipedia.org/wiki/Trie)
to compute common prefixes for hostnames, these are used to help formulate the
rules we eventually create.

The error produced is expected, this is simply what is generated when a
particular rule fails the ratio test mentioned above. Note that there are
multiple attempts to transform a given closure into a rule, so just because this
particular attempt failed does not mean the data won't be used.

Once the script has finished, we can see the rules that got generated:

```
$ wc -l adobe.rules
6215 adobe.rules
```

Some of these might seem silly (and maybe they are?), but we will examine the
results shortly and see how they fared.

## Generating a brute-force list

Now that we have the rules, we need to generate our brute-force list, we simply
run the included `make_brute_list.sh` script:

```
$ ./make_brute_list.sh adobe.rules adobe.brute
```

```
$ wc -l adobe.brute
124821 adobe.brute
```

```
$ head adobe.brute
19-da-tryit.adobe.com
19-da-tryit1.adobe.com
19-da-tryit2.adobe.com
19-da-vip.adobe.com
19-da-vip1.adobe.com
19-da-vip2.adobe.com
19-da1.adobe.com
19-da11.adobe.com
19-da12.adobe.com
19-origin-tryit.adobe.com
```

## Evaluation against `altdns`

I think the `altdns` tool (https://github.com/infosec-au/altdns) makes for an
apt comparison. Both tools have a similar purpose: given some input DNS names
both produce mutated names as output for use in a DNS brute-force.

Here is how I generated the `altdns` list (where `adobe` is the same output from
`amass` used above):

```
$ python3 altdns/altdns -i f500/adobe -o adobe_altdns -w altdns/words.txt
```

```
$ wc -l adobe_altdns
3619334
```

Here's is the non-scientific methodology I used for comparison:

1. Use a DigitalOcean VPS

2. Use the `dnsvalidator` (https://github.com/vortexau/dnsvalidator) tool to
collect valid public DNS resolvers

3. Use the `puredns` (https://github.com/d3mondev/puredns) tool with the public
resolvers from [2] for DNS resolution

4. Deduplicate results against what we had originally from `amass`

5. Re-collect resolvers and wait 30 mins between runs

## Results

Here are the results I obtained:

- For `124,821` guesses, regulator captured `1242` new hostnames
- For `3,619,334` guesses, `altdns` captured `362`

I'm not going to try to interpret the results too much, but I think it's fair to
say that regulator "won" this round in absolute numbers.

# Conclusion

I've attached some more trials I collected between regulator, `altdns` and
`dnsgen` (https://github.com/ProjectAnte/dnsgen).

Regulator does seem to be fairly "efficient" depending on how you want to count,
but it still loses in general to `dnsgen` (I also used the `--fast` flag for
`dnsgen`).

Overall, I'm happy with the results of this project, I got to learn some cool
stuff and hopefully inspire others to take up using `dank`.

- https://github.com/cramppet/dank
- https://github.com/cramppet/regulator

![More regulator results](./regulator_res2.png)